2-2430026 info@educenter.es

eduGMAT mini-test 1: Arithmetic

by | Jul 11, 2018 | GMAT, GRE |

eduGMAT mini-test 1: Arithmetic

eduGMAT® mini-test 1: Arithmetic Exercises

Numbers
Numbers are classified according to their type. The first type is the one you have known since elementary school:
Natural numbers (whole positive numbers) – are the numbers used for counting: 1, 2, 3, 4, 5, … Adding 0 and the negatives of the naturals, we obtain
Integers – numbers from the set {…, -2, -1, 0, 1, 2, 3, 4, 5, … }
Note: The integer 0 is neither positive nor negative. 

[qsm quiz=15]

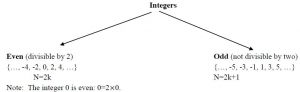
Properties of even/odd integers
even × even = even
even × odd = even
odd × odd = odd
even +/− even = even
odd +/− odd = even
odd +/− even = odd
even/odd = even or not integer
even/even = even or odd or not integer
odd/odd = odd or not integer

[qsm quiz=16]

The numbers –2, –1, 0, 1, 2, 3, 4, 5 are consecutive integers. Consecutive integers can be represented by n, n + 1, n + 2, n + 3, . . . , where n is an integer.
The numbers 0, 2, 4, 6, 8 are consecutive even integers. Consecutive even integers can be represented by 2n, 2n + 2, 2n + 4, . . . , where n is an integer.
The numbers 1, 3, 5, 7, 9 are consecutive odd integers. Consecutive odd integers can be represented by 2n + 1, 2n + 3, 2n + 5, . . . , where n is an integer.
Note: if the numbers are given in the problem in a raw like a, b, c it does not mean that a<b<c.
Properties:

    • for every two consecutive integers n and n + 1 product n ∙ (n + 1) is divisible by 2;
    • for every three consecutive integers n, n + 1, n + 2 product n ∙ (n + l) ∙ (n + 2) is divisible by 3 and by 2;
    • for every k consecutive integers their product is divisible by all numbers from 1 to k.

[qsm quiz=17]

A prime number is a positive integer that has exactly two different positive divisors: 1 and itself.
For example, 2, 3, 5 are prime numbers, but 15 is not, since 15 has four different positive divisors, 1, 3, 5, and 15.
First prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47…
Note: If the number less than 100 is not divisible by 2, 3, 5, 7, it is prime.
Note: The number 1 is not a prime number since it has only one positive divisor.
Note: 2 is the only even prime. Indeed, if a prime greater than 2 were even, it would have at least three different divisors: 1, itself and 2.

[qsm quiz=18]

468