2-2430026 info@educenter.es

eduGMAT mini-test 1: Aritmética

por | Jul 12, 2018 | GMAT, GRE |

eduGMAT mini-test 1: Aritmética

eduGMAT® mini-test 1: Ejercicios de Aritmética

Números
Los números se clasifican de acuerdo a su tipo. El primer tipo es el que conoces desde la escuela primaria:
Números naturales(números positivos enteros) – son los números utilizados para contar: 1, 2, 3, 4, 5, … Añadiendo 0 y los negativos de los naturales, obtenemos
Enteros: – números del conjunto {…, -2, -1, 0, 1, 2, 3, 4, 5, …}
Nota: El número entero 0 no es positivo ni negativo.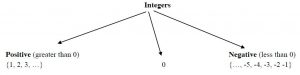 

[qsm quiz=15]

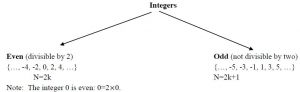
Propiedades de enteros pares/impares
par × par = par
par × impar = par
odd × impar = impar
par +/− par = par
impar +/− impar = par
impar +/− par = impar
par/odd = par or not integer
par/par = par or impar or not integer
odd/odd = impar or not integer

[qsm quiz=16]

Los números –2, –1, 0, 1, 2, 3, 4, 5 son enteros consecutivos. Los enteros consecutivos se pueden representar por n, n + 1, n + 2, n + 3,. . . , donde n es un número entero.
Los números 0, 2, 4, 6, 8 son enteros consecutivos pares. Los enteros par consecutivos se pueden representar por 2n, 2n + 2, 2n + 4,. . . , donde n es un número entero.
Los números 1, 3, 5, 7, 9 son enteros consecutivos impares. Los enteros impares consecutivos se pueden representar por 2n + 1, 2n + 3, 2n + 5,. . . , donde n es un número entero.
Nota: si los números se dan en el problema en un crudo como a, b, c, no significa que a Propiedades:

    • por cada dos enteros consecutivos n y n + 1 producto n ∙ (n + 1) es divisible por 2;
    • por cada tres enteros consecutivos n, n + 1, n + 2 producto n ∙ (n + l) ∙ (n + 2) es divisible por 3 y por 2;
    • por cada k enteros consecutivos, su producto es divisible por todos los números desde 1 hasta k.

[qsm quiz=17]

Un número Primo es un entero positivo que tiene exactamente dos divisores positivos diferentes: 1 y sí mismo..
Por ejemplo, 2, 3, 5 son números primos, pero 15 no, ya que 15 tienen cuatro divisores positivos diferentes, 1, 3, 5 y 15.
Los primeros números primos son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 …
Nota: Si el número de menos de 100 no es divisible por 2, 3, 5, 7, es primo.
Nota: El número 1 no es un número primo ya que solo tiene un divisor positivo.
Nota: 2 es el único primo par. De hecho, si un primo mayor que 2 fuera par, tendría al menos tres divisores diferentes: 1, sí mismo y 2.

[qsm quiz=18]

468